In deze sectie vindt u een theoretische uitleg van een aantal facetten en termen uit de reologie en viscositeit. Aangezien er een hoop onduidelijkheid is over verschillende termen en eenheden in de reologie worden deze extra toegelicht.
De Wet van Newton
In de reologie wordt veel gesproken over Newtonse en niet-Newtonse vloeistoffen. Om deze termen de begrijpen is het noodzakelijk om de term Newton nader te verklaren. Lees verder…
Deze term komt uit de Wet van Newton, deze zegt:
“De viscositeit van een vloeistof is een constante. Als de afschuifsnelheid verandert, verandert de afschuifspanning evenredig, zodat de viscositeit constant is.” Hier wordt bedoeld dat we spreken van een vloeistof die voldoet aan de Wet van Newton (Newtonse vloeistof) niet van viscositeit verandert op het moment dat de afschuifsnelheid gewijzigd wordt. Als we spreken van relatieve (Brookfield) viscositeit, houdt dit in dat als we het toerental wijzigen, de viscositeit constant blijft.
Enkele voorbeelden van Newtons vloeistoffen zijn:
- water
- glycerine
- minerale olie
- oplosmiddelen
Op het moment dat een vloeistof niet aan deze wet voldoet, spreken we van een niet-Newtonse vloeistof. Dit betekent dat als we de afschuifsnelheid aanpassen, de viscositeit zal stijgen of dalen. Dit geldt voor de meeste applicaties. Meestal wordt dit veroorzaakt door een interne structuur in het materiaal.
Bij dit soort vloeistoffen dient er dus rekening mee gehouden te worden met welke afschuifsnelheid of toerental er gemeten dient te worden. Indien de gegevens gecommuniceerd worden naar een andere partij, is het dus ook essentieel dat de afschuifsnelheid of toerental vermeld is.
Samengevat:
Indien de viscositeit wordt gemeten bij verschillende afschuifsnelheden en de viscositeiten zijn gelijk, dan heeft het materiaal Newtonse eigenschappen over het afschuifsnelheidsgebied waar het werd gemeten.
Absolute en relatieve viscositeit
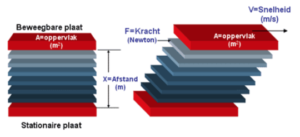
Bij het bovenstaand model, dat beschreven is door Newton gaat men er van uit, dat de afstand tussen de platen (X) relatief klein is. Daarbij zijn de beschreven parameters, zoals snelheid en oppervlakte van de platen tevens exact bekend.
Zou men viscositeit meten met een viscositeitmeter, die aan bovenstaande voorwaarden zou voldoen dan meet men de zogenaamde absolute viscositeit.
Vele viscositeitmeters echter, meten de zogenaamde relatieve viscositeit. Hierbij zijn juist de afstand tussen de platen, (afschuif)snelheid en oppervlak niet exact gedefinieerd. Bij relatieve viscositeit vergelijkt men feitelijk de “weerstand” van de vloeistof met die van een vastgestelde en traceerbare viscositeitstandaard.
Bij een vloeistof, die zich Newtons gedraagt en waarbij de viscositeit onafhankelijk is van de afschuifsnelheid zal de absolute viscositeit en relatieve viscositeit niet verschillen.
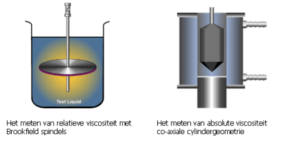
Bij een rotatieviscositeitmeter zijn vaak standaard (Brookfield)spindels geleverd. Typerend voor deze spindels is het feit, dat hiermee relatieve viscositeit wordt gemeten. Immers, afstand tussen de platen (in dit geval spindel en wand van een bekerglas) is niet meer verwaarloosbaar klein en volstrekt willekeurig. Hierdoor zijn dus afschuifsnelheid en -spanning niet gedefinieerd.
Om met een rotatieviscositeitmeter absolute viscositeit te meten bestaan accessoires met bijvoorbeeld co-axiaiale cilinder- of kegel/plaat-geometrieen. Elke Brookfield viscositeitmeter kan hiermee worden uitgerust.
Kinematische viscositeit:
De viscositeit η wordt ook wel dynamische viscositeit genoemd.
De viscositeit kan ook op andere manieren worden gemeten zoals met een uitstroombeker, of een capillair viscositeitmeter.
Hierbij wordt de uitstroomsnelheid gemeten die uiteraard afhankelijk is van de zwaartekracht. Eén van de parameters die dan van belang zijn is o.a. de dichtheid van de vloeistof. Deze viscositeit noemen we de kinematische viscositeit, ν (Gr. letter, nu). De kinematische viscositeit wordt gedefinieerd als het quotient van de dynamische viscositeit η (N.m−2.s) en de dichtheid ρ (kg.m−3)(Gr. letter, rho) van de vloeistof:
ν = η / ρ (cm2/s) = Stokes
Afschuifspanning en afschuifsnelheid
Het stromingsgedrag van een vloeistof kan beschreven worden aan de hand van het zogenaamde model van Newton.
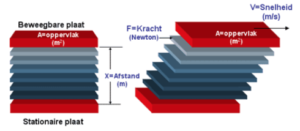
Stel dat een vloeistof zich tussen twee platen bevindt. De afstand tussen de twee platen bedraagt x (m). De bovenste plaat heeft een oppervlakte A (m2). Stel dat deze plaat zich naar rechts beweegt, terwijl de onderste plaat stil staat. In de bewegingsrichting van de bovenste plaat werkt een kracht F (N). Deze kracht zorgt ervoor, dat de snelheid van de bovenste plaat, gedefinieerd als V (m/s) constant is. De snelheid van de vloeistof is niet overal hetzelfde maar is afhankelijk van de plaats in de vloeistof laag. Op de onderste plaat is de snelheid 0 terwijl ter hoogte van de bovenste plaat deze V bedraagt. Afhankelijk van de plaats tussen de twee platen bestaat er dus een verdeling van snelheid, die de snelheidsgradient wordt genoemd.
Deze snelheidsgradient kan worden uitgedrukt als de verandering van de snelheid (dV) als functie van de plaats tussen de platen (dX). Dit noemen we de afschuifsnelheid (‘shear rate’) die wordt aangeduid met ỳ (uitgesproken als gamma punt):
ỳ = snelheidsgradient = dV/dX
ỳ = V (m/s) / x (m)
ỳ = afschuifsnelheid (s-1)
De kracht, die gerelateerd is aan het oppervlak van de bewegende plaat, wordt afschuifspanning (‘shear-stress’), genoemd. Deze laatste wordt aanduid met de Griekse letter τ (tau):
τ = kracht / oppervlakte eenheid
ofwel
τ = F / A (in N / m2) = Pa (Pascal)
Bij een vloeistof wordt de relatie tussen de afschuifspanning (τ) en afschuifsnelheid (ỳ) gedefinieerd door de viscositeit η:
η = afschuifspanning / afschuifsnelheid
η = Pa / s-1 = Pa . s
Flowcurves
Zoals elders beschreven, zijn er een verschillende parameters die invloed op de viscositeit van een stof kunnen hebben. Alle parameters kunnen, afhankelijk van het soort te meten product, een verschillende uitwerking hebben. Om de stromingseigenschappen van een vloeistof onder invloed van verschillende parameters duidelijk in beeld te brengen, wordt er veelal gebruik gemaakt van viscositeitscurves.
Aan de hand van deze viscositeitscurves staan hieronder enkele verschillende stromingseigenschappen, ingedeeld onder de verschillende parameters.
Parameter: Afschuifsnelheid
Newtons stromingseigenschap
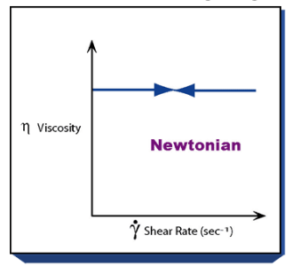
Toelichting
Ongeachte met welke afschuifsnelheid (shear rate) er gemeten wordt, zal de viscositeit altijd constant zijn.
Pseudoplastische stromingseigenschap
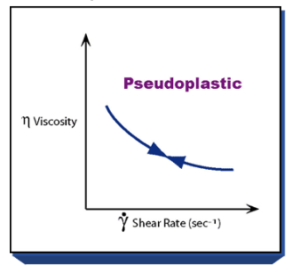
Toelichting
Op het moment dat de afschuifsnelheid (shear rate) verhoogd wordt, zal de viscositeit dalen en vice versa. Hier spreekt men ook wel van shear-thinning.
Dilatante stromingseigenschap
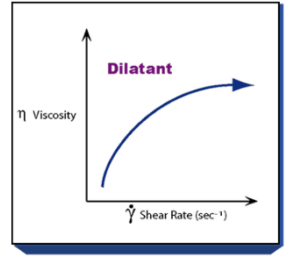
Toelichting
Op het moment dat de afschuifsnelheid (shear rate) verhoogd wordt, zal de viscositeit stijgen en vice versa. Hier spreekt met ook wel van shear-thickening.
Parameter: Tijd
Tixotrope stromingseigenschap
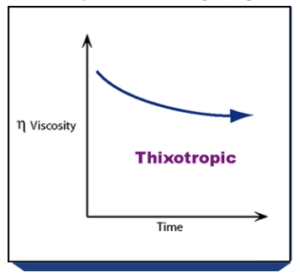
Toelichting
Op het moment dat de viscositeit gemeten wordt onder een vaste afschuifsnelheid en voor langere tijd, zal de viscositeit dalen.
Reopectische stromingeigenschap
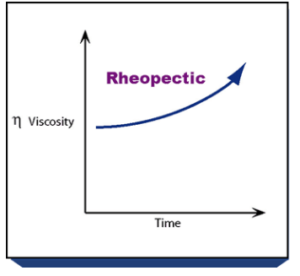
Toelichting
Op het moment dat de viscositeit gemeten wordt onder een vaste afschuifsnelheid en voor langere tijd, zal de viscositeit stijgen.
Parameter: Temperatuur
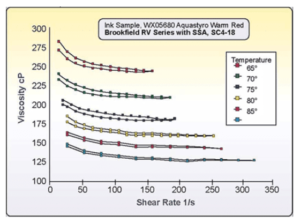
Toelichting
Veel producten hebben de eigenschap om bij een hogere temperatuur een lagere viscositeit te hebben.

